https://www.acmicpc.net/problem/4013
4013번: ATM
첫째 줄에 교차로의 수와 도로의 수를 나타내는 2개의 정수 N과 M(N, M ≤ 500,000)이 차례로 주어진다. 교차로는 1부터 N까지 번호로 표시된다. 그 다음 M개의 줄에는 각 줄마다 각 도로의 시작 교차
www.acmicpc.net
사용 알고리즘
SCC + 위상정렬 DP
풀이
ATM에서 현금을 인출할 때, 어떤 정점에서 사이클이 존재한다면 그 사이클을 쭉 돌면서 사이클에 속하는 모든 정점의 ATM을 이용할 수 있다. 따라서 사이클 내의 정점들을 묶어 생각할 수 있고, 하나의 SCC로 묶어줄 수 있음을 알 수 있다.
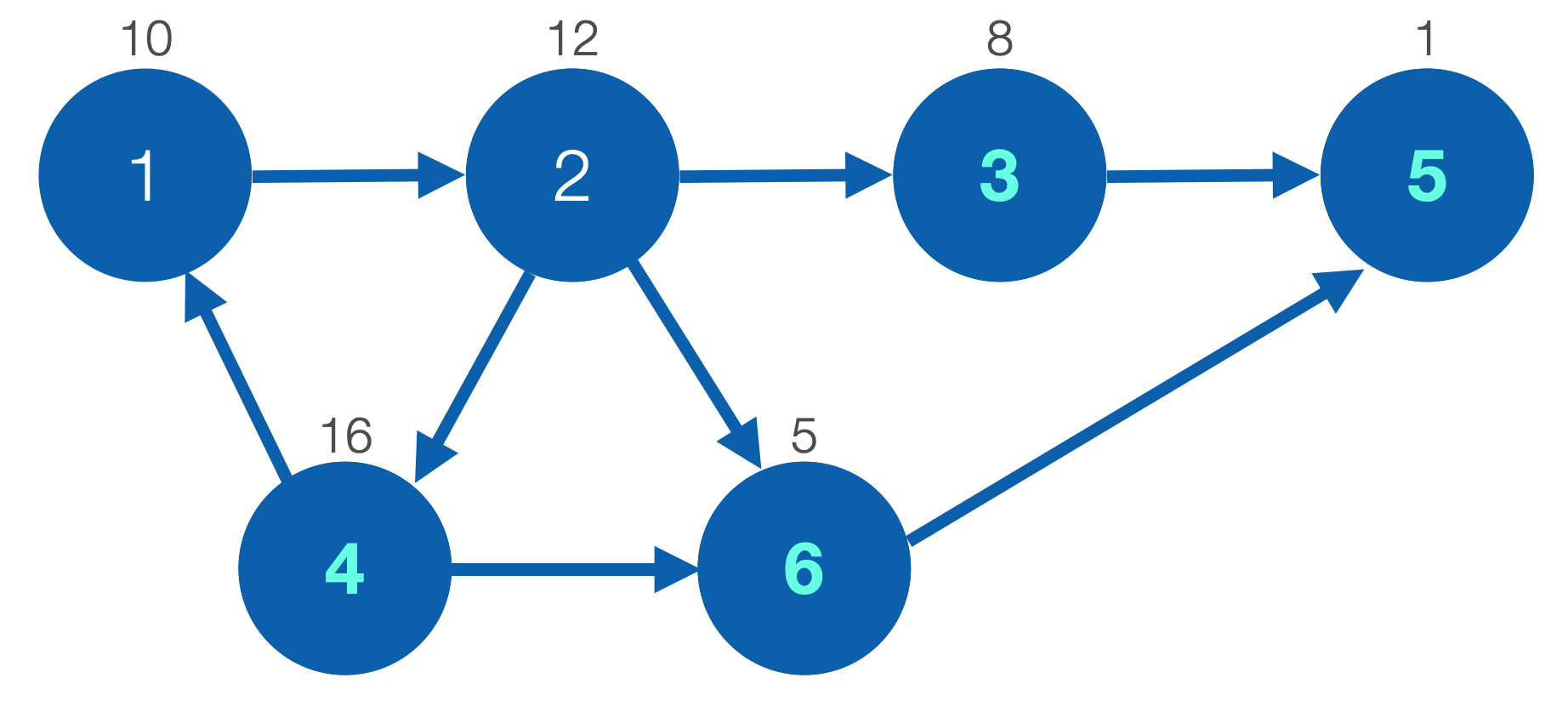
예제 그래프이다. 위에 적힌 숫자는 ATM에서 인출할 수 있는 현금이고, 색칠된 숫자는 그 정점에 레스토랑이 있다는 뜻이다.
여기서 {1,2,4}, {3}, {5}, {6}으로 SCC를 분리할 수 있으며, 그 결과는 아래와 같다.
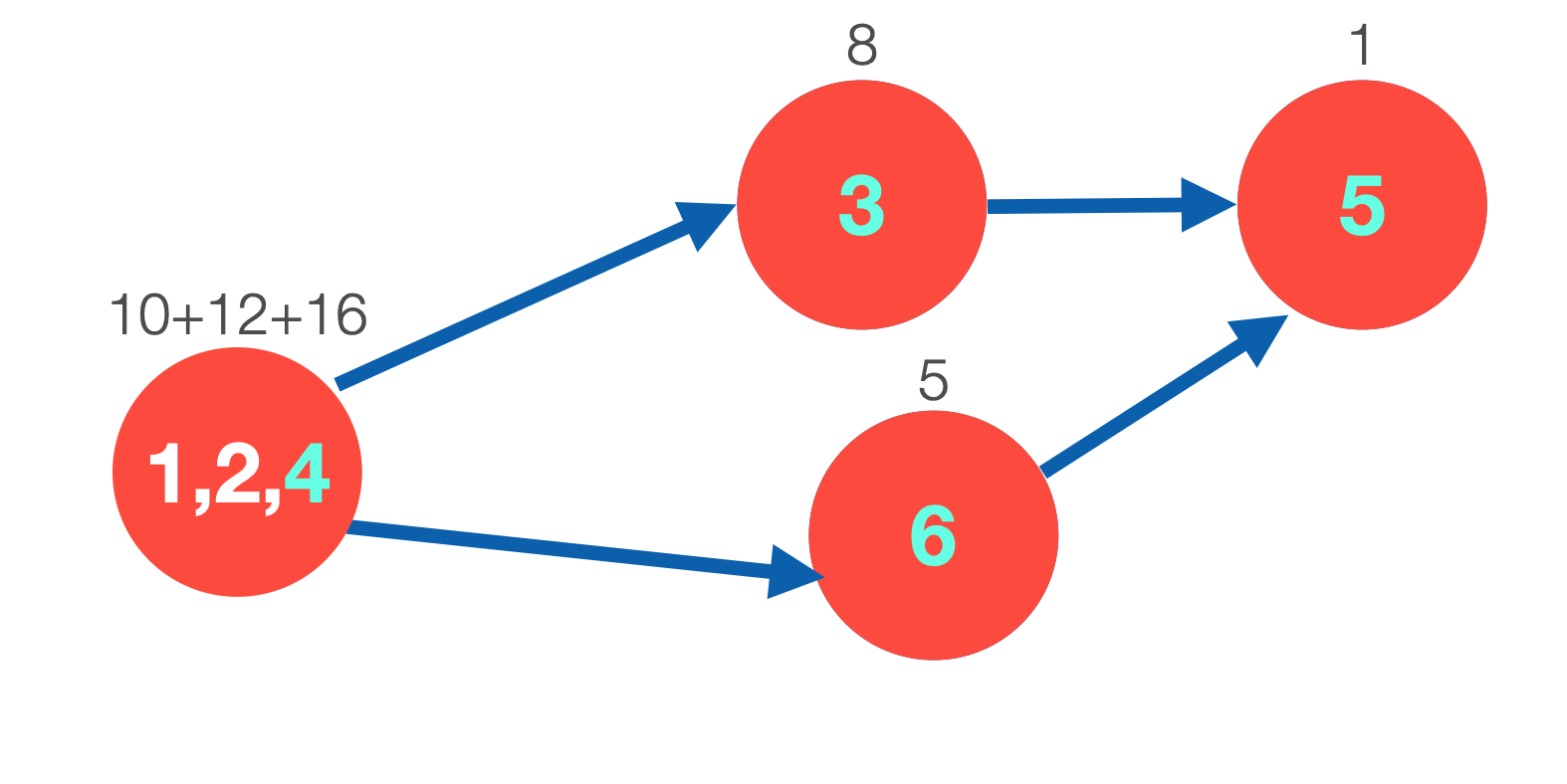
각 SCC에서 인출할 수 있는 현금은 SCC에 속하는 인출할 수 있는 현금의 합이며, 레스토랑의 존재 여부는 SCC에 속하는 정점 중 하나 이상이 레스토랑에 속하는지에 따라 결정된다.
이 SCC 그래프 상에서 indegree가 0인 정점들을 기준으로 위상 정렬을 실시하고, 다음과 같은 DP 테이블을 채워 나간다.
dp[i] := i번 SCC까지 오면서 인출할 수 있는 최대 현금
위 그림에서 {1,2,4}는 1번, {3}은 2번, {6}은 3번, {5}는 4번 SCC라 하자.
dp[i]는 다음과 같이 계산된다.
$$ dp[i] = \underset{j\in prv(i)}{max}(dp[j]) + cost[i] $$
(prv(i) : i로 진출하는 정점 ex)prv(2) = {1}, prv(4) = {2,3})
(cost[i] : i번 SCC에서 인출할 수 있는 현금)
dp 값을 위상정렬 순서대로 계산하고, 레스토랑이 존재하는 SCC에서만 답을 구하면 최댓값을 구할 수 있다.
#include <iostream>
#include <cmath>
#include <algorithm>
#include <numeric>
#include <cstring>
#include <vector>
#include <string>
#include <climits>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <bitset>
#include <cassert>
#include <list>
using namespace std;
#define fast ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0)
#define all(x) x.begin(), x.end()
#define rll(x) x.rbegin(), x.rend()
#define comp(x) x.erase(unique(all(x)), x.end())
#define MOD 1000000007
typedef long long ll;
ll n, m;
ll dp[505050];
ll sccn[505050], dfsn[505050], scnt, cnt;
ll s[505050], top;
bool finished[505050];
bool is_restaurant[505050], is_restaurant_scc[505050];
ll cost[505050], cost_scc[505050];
vector<ll> adj[505050], adj_scc[505050];
ll ind_scc[505050];
ll dfs(ll cur){
dfsn[cur] = ++cnt;
s[++top] = cur;
ll res = cnt;
for(auto next : adj[cur]){
if(!dfsn[next])res = min(res, dfs(next));
else if(!finished[next])res = min(res, dfsn[next]);
}
if(res==dfsn[cur]){
scnt++;
ll c = 0;
bool flag = 0;
while(1){
ll x = s[top--];
finished[x]=1;
sccn[x] = scnt;
c += cost[x];
flag |= is_restaurant[x];
if(x==cur)break;
}
cost_scc[scnt] = c;
is_restaurant_scc[scnt]=flag;
}
return res;
}
ll S, p;
int main(){
fast;
cin>>n>>m;
for(int i = 0 ; i < m ; i++){
ll a,b; cin>>a>>b; adj[a].push_back(b);
}
for(int i = 1 ; i <= n ; i++)cin>>cost[i];
cin>>S>>p;
for(int i = 0 ; i < p ; i++){
ll a; cin>>a;
is_restaurant[a]=1;
}
for(int i = 1 ; i <= n ; i++)if(!dfsn[i])dfs(i);
for(int i = 1 ; i <= n ; i++){
for(auto next : adj[i]){
if(sccn[i]==sccn[next])continue;
adj_scc[sccn[i]].push_back(sccn[next]);
ind_scc[sccn[next]]++;
}
}
queue<ll> q;
vector<bool> chk(scnt+1, 0);
chk[sccn[S]]=1;
for(int i = 1 ; i <= scnt ; i++){
if(ind_scc[i]==0)q.push(i);
}
ll ans = 0;
while(q.size()){
ll cur = q.front();
q.pop();
dp[cur] += cost_scc[cur];
for(auto next : adj_scc[cur]){
chk[next] = (chk[next] | chk[cur]);
if(chk[cur])dp[next] = max(dp[next], dp[cur]);
if(--ind_scc[next]==0){
q.push(next);
}
}
}
for(int i = 1 ; i <= scnt ; i++){
if(is_restaurant_scc[i] and chk[i])ans = max(ans, dp[i]);
}
cout<<ans;
}
'백준 > 플래티넘' 카테고리의 다른 글
| BOJ 25639 - 수열과 최대 상승 쿼리 (P1) (0) | 2023.08.14 |
|---|---|
| BOJ 1201 - NMK (P3) (0) | 2023.07.22 |
| BOJ 25405 - 레벨 업 (P1, KOI 2022 중등부 4, 고등부 3) (0) | 2023.07.01 |
| BOJ 1395 - 스위치 (P3) (0) | 2023.06.28 |
| BOJ 18770 - 불안정한 물질 (P2) (0) | 2023.06.14 |


